La ley de los signos de matemáticas: suma, resta, multiplicación y división (reglas)

La ley de los signos matemáticos es el conjunto de reglas básicas para efectuar las operaciones aritméticas. Si se siguen dichas normas, se consiguen resultados fiables.

Estas normativas afectan si un número positivo o negativo queda de esta manera o se convierte en otro valor sujeto a los valores que la anteceden.

Los signos matemáticos son aquellos que simplifican y dan orden lógico a cualquiera de las tantas operaciones aritméticas de primer, segundo y tercer grado.

Si bien es cierto, la matemática es una ciencia que utiliza axiomas para entender el modus operandi de las propiedades, teoremas, fracciones y definiciones de todo el entorno, al mismo tiempo, los signos matemáticos buscan un razonamiento lógico en sus procesos para conformar teorías básicas y respuestas en la vida diaria.

Las leyes de los signos de matemáticas son utilizados en toda la secciones de la vida, bien sea para sacar la suma de un producto a la división de una cuenta entre amigos a la hora de salir a comer

Ley de los signos de matemáticas

La suma

Para esta ley existen algunas normas como:

• Los números que no tengan un signo delante, se entiende que es positivo. No hace falta que se escriba.
• Si ambos números son positivos, el resultado es positivo, paralelamente, a la variable que dé la operación.
• De ser un número negativo con otro negativo en una suma, el número resultante será negativo.

Ejemplos:

• 5 + 5 = 10
• (-3) + (-2)= -5
• -7 + 4= -3

La resta

Las condiciones matemáticas dentro de una operación negativa son muy similares a las que realizan durante una suma.

Ejemplos:

• (+6) – (+2)= +4
• (-7) – (-4)= -3

La multiplicación y la división

En este caso, la ley de los signos de matemáticas cambia exponencialmente debido a la diversidad en las variables, quedando de la siguiente manera:

• En el caso de dos números positivos, a la hora de multiplicar y dividir el resultado es positivo.
• Mientras que los números negativos con negativos, al momento de dividir y multiplicar el resultado será negativo.
• En el caso de los números negativos con positivos serán tomado el signo con mayor valor a la hora de la operación.

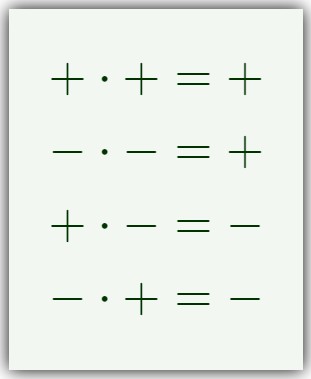
Ejemplo:

• (+6) ÷ (+4)= +1,5
• (-8) ÷ (-4)= +2
• (+4) ÷ (-2)= -2

Estos son los signos matemáticos con los que se pueden aplicar las reglas

Las leyes son comúnmente utilizadas para los siguientes signos de matemáticas para la conformación de operaciones más sencillas y prácticas. Entre ellos están:

Suma (+)

El signo matemático de la suma (+) es aquel que representa una adición o incorporación de uno o varios elementos a una cierta cantidad. Ejemplo

• 4 + 4 = 8
• 2 + 2 = 4
• 20 + 10 = 30

Resta (-)

El signo matemático de la resta (-) es aquel que se encarga de sustraer o quitar elementos de una operación. Ejemplo:

• 2 - 2 = 0
• 10 - 5 = 5
• 25 - 4 = 21

Multiplicación (X, *)

El signo de la multiplicación (X, *) no es más que la cantidad de veces que se debe sumar un determinado número. Ejemplo: 3 x 4 = 3 + 3 + 3 + 3

Sin embargo, se expresa de la siguiente manera: 3 x 4 = 14

La multiplicación también es conocida por contener un asterisco (*) para realizar las operaciones. Ejemplo: 3*4 = 12.

División (/, ÷)

El signo matemático de división (/, ÷) es la encargada de la repartición de una suma en igualdad de partes. Ejemplo:

• 10/ 2 = 5
• 20/10 = 2
• 35/5 = 7

Igual  (=)

El signo matemático de igual (=) es aquel que se utiliza para brindar una especie de equilibrio o el resultado de una operación matemática.

Para los expertos en las ciencias exactas, el signo igual es el más importante de toda la clasificación. Ejemplo:

• 5 + 6 = 11
• 6 – 2 = 4
• 5/5 = 1

Paréntesis, corchete y llaves (( ), [ ] , { })

Los signos matemáticos paréntesis, corchete y llaves (( ) , [ ] , { }) son ideales para agrupar y ordenar algunas operaciones cuando están en una misma operación aritmética. Ejemplo:

• 10 ÷ (5 - 3)
• 23 * [ X – ( 5 – 3) + 5]

Cuando se esté frente a estos problemas, es ideal resolver lo que está adentro para proseguir con los valores externos.

Guía práctica: ¿Cómo entender la ley de los signos matemáticos?

Una vez explicado todos los aspectos básicos es importante saber que el entendimiento de la ley de los signos de matemáticas se fundamenta en condiciones y reglas.

La ley de los signos matemáticos se rige para que todos los números se multipliquen según el orden de su posición.

La ley se basa en:

• Signos iguales convierten el número en positivo, es decir que (+) por (+) el resultado siempre será positivo.
• Signos diferentes el resultados será según las variables en la ecuación, es decir que si el número es (-) con otro (-) el resultado será positivos.
• Pero si el número es (+) y el otro número es (-) el resultado será negativo, igualmente aplica  a la inversa.

Objetivo de la ley de los signos de matemáticas

La importancia de las leyes de los signos de matemáticas reside en los resultados lógicos que surgen de estas operaciones aritméticas.

El entendimiento de las normativas es casi obligatorio e intuitivo mientras un individuo va creciendo debido a la integración con las matemáticas básicas y operaciones más sencillas.

Su importancia también reside en la necesidad del hombre con elementos abstractos  en el ordenamiento lógico para el uso de procedimientos tecnológicos y otras ramas de conocimiento.

Muchos de los expertos aseguran que las matemáticas como tal no tienen leyes si no una serie de normativas y condiciones para poder realizar mejor las operaciones.  

Es válido acotar que los estudios matemático deben ser realizados con muchas meticulosidad debido a que un mal cálculo podría ocasionar muchos problemas y malos entendidos.